Note de curs, clasele 9-12, 20 martie 2014
Discutarea temei
Nu încă. ;-)
RMQ restricționat
Din lecția de data trecută a rămas de predat ultima secțiune, rezolvarea RMQ restricționat în < O(n), O(1), O(n) >.
Geometrie computațională (introducere)
Aceasta este a 5-a lecție de geometrie computațională predată în ultimele 18 luni. Mereu însă au fost lecții speciale, cu toate clasele, forțate de împrejurări. De aceea, vom reîncepe cu noțiunile introductive.
Aplicații
Geometria computațională are nenumărate aplicații în informatică:
- robotică, roboți autonomi, machine vision
- grafică 2D (hărți, GPS, probleme de vizibilitate pe segmente și dreptunghiuri)
- grafică 3D (jocuri)
- modelarea 3D a moleculelor în căutarea de medicamente
Elemente de geometrie analitică
Ecuația dreptei
Ecuația dreptei poate fi exprimată în multe forme:
- este dreapta care trece prin punctele și .
- este dreapta care trece prin punctul și are pantă . Panta este tangenta unghiului format de dreaptă cu axa Ox.
- (numită în engleză slope + y-intercept) este dreapta care trece prin punctul și are pantă .
- (numită în engleză x-intercept + y-intercept) este dreapta care taie axele Ox și Oy în punctele și
Aceste formule se demonstrează prin asemănarea triunghiurilor dreptunghice. Toate se pot rescrie în forma generală a ecuației dreptei,
De expandat: ecuații parametrice și vectoriale.
Panta unei drepte
Dându-se o dreaptă prin ecuația generală ax + by + c = 0, panta dreptei este . Putem observa aceasta rescriind ecuația ca , care corespunde formei slope + y-intercept.
Intersecția a două drepte
Date fiind două drepte, ax + by + c = 0 și dx + ey + f = 0, punctul lor de intersecție se determină, evident, rezolvând sistemul de ecuații în x și y.
Drepte paralele, perpendiculare
Două drepte sunt paralele când formează unghiuri egale cu orizontala, adică au pante egale: sau
Două drepte sunt perpendiculare când produsul pantelor este egal cu -1: sau
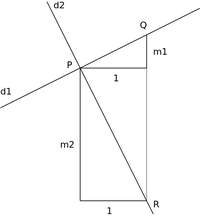
Schiță de demonstrație: vezi figura. Fie dreptele și cu pantele și . Din punctul de intersecție, P, construim punctele Q și R. Remarcăm că Q și R sunt pe aceeași verticală. Reținem că este negativ. Cum triunghiul PQR este dreptunghic, aplicăm teorema lui pitagora:
Separarea planului
Evident, expresia ax + by + c va fi zero pentru toate punctele (x, y) de pe dreaptă (în mod tautologic). Ce este interesant este că expresia are valori pozitive pentru toate punctele de o parte a dreptei și valori negative pentru toate punctele de cealaltă parte a dreptei.
De care parte? Nu putem spune exact, căci dreapta ax + by + c este confundată cu dreapta - ax - by - c, care are semnele schimbate. Dar tot ce contează este ca programul vostru să proceseze consecvent toate dreptele.
Test de orientare
O întrebare frecventă este: dându-se trei puncte A, B, și C, sunt ele (a) date în ordine trigonometrică sau (b) date în ordine orară sau (c) coliniare?
Putem reformula întrebarea în două feluri echivalente:
- Dându-se A, B și C, segmentul BC cotește, față de segmentul AB, (a) la stânga sau (b) la dreapta sau (c) nu cotește?
- Dându-se A, B și C, punctul C este, față de segmentul orientat AB, (a) la stânga sau (b) la dreapta sau (c) pe linie?
Putem răspunde la întrebare muncitorește: calculăm ecuația dreptei AB sub forma ax + by + c = 0 și înlocuim coordonatele punctului C în această ecuație. Mai simplu, Pornim de la ecuația dreptei care trece prin două puncte, trecem totul în partea stângă și înlocuim x și y cu xC și yC. Obținem:
Putem exprima mai elegant această formulă printr-un determinant:
- Dacă determinantul este pozitiv, punctele sunt date în ordine trigonometrică (traiectoria ABC cotește la stânga).
- Dacă determinantul este negativ, punctele sunt date în ordine orară (traiectoria ABC cotește la dreapta).
- Dacă determinantul este zero, punctele sunt coliniare.
Observații privind implementarea
Cazuri particulare
O bună parte din arta implementării unui algoritm de geometrie computațională este tratarea cazurilor particulare:
- coliniaritate
- intersecții exact la un capăt al segmentului
- pante infinite (pentru drepte verticale)
Uneori puteți elimina cazurile particulare scriind bine formula. Exemplu: două puncte și sunt coliniare cu originea dacă . Dar această formulă are cazuri particulare: fracțiile sunt nedefinite când sau sunt 0. Așadar, implementarea de mai jos este greșită.
if (y1 / x1 == y2 / x2) {
...
}
Putem trata punctele de pe axa Ox printr-un caz particular, sau, mai simplu, putem înlocui formula cu una echivalentă, dar fără împărțiri:
if (y1 * x2 == y2 * x1) {
...
}
De expandat: Funcții ca atan2(), care gestionează și cazuri particulare.
Erori de calcul
În gcc, tipurile float, double și long double au 4, 8 și respectiv 16 octeți. Țineți minte aceste numere ca să vă puteți face necesarul de memorie.
Indiferent de precizie, în funcție de problemă puteți ajunge la valori ușor diferite pentru formule teoretic egale, în funcție de ordinea operațiilor. De aceea poate fi mai sănătos să nu testați egalitatea cu
if (x == y) {
...
}
, ci cu
if (fabs(x - y) < 1e-5) {
...
}
Funcțiile de valoare absolută sunt fabsf() pentru float, fabs() pentru double și fabsl pentru long double. Încă un motiv să lucrați în GNU/Linux, nu în Windows: paginile de manual includ toată documentația pentru GCC.
Operații costisitoare
Țineți minte că adunarea / scăderea, înmulțirea, împărțirea, sqrt, sin / cos, log / exp sunt funcții tot mai costisitoare. Întrebați-vă mereu cum puteți rescrie o formulă pentru a folosi operații cât mai de la începutul listei.
Algoritmul lui Bresenham (pentru segmente)
Pentru a exemplifica observațiile de mai sus, vom discuta algoritmul lui Bresenham. El trasează un segment între doi pixeli (puncte de coordonate întregi) (x1, y1) și (x2, y2). Se pune, deci, problema enumerării tuturor pixelilor segmentului.
Pentru simplitate, presupunem că segmentul este în primul octant, adică formează un unghi între 0 și 45° cu orizontala. Celelalte 7 cazuri se tratează similar. Ce este special în primul octant? După afișarea punctului (x, y), următorul punct afișat va fi fie (x + 1, y), fie (x + 1, y + 1). Deci algoritmul are de luat o decizie relativ ușoară la fiecare avansare a lui x.
Algoritmul naiv spune: datorită unghiului, toți pixelii au coordonata x diferită. Iterăm deci de la x1 la x2 și calculăm coordonata y corectă pe acea coloană. Ea se obține rotunjind coordonata y teoretică la cel mai apropiat întreg.
for (int x = x1; x <= x2; x++) {
y = (double)(y2 - y1) / (x2 - x1) * (x - x1) + y1;
int yint = round(y);
// afișează pixelul (x, yint)
}
Acest algoritm face împărțiri pe numere reale, care sunt scumpe.
O variantă mai bună precalculează panta și face împărțiri și înmulțiri înainte de bucla principală, iar în buclă face doar adunări. Ideea este că, de câte ori x crește cu 1, y crește cu valoarea pantei. Apoi y este rotunjit la cel mai apropiat inel.
double p = (double)(y2 - y1) / (x2 - x1);
double y = y1;
for (int x = x1; x <= x2; x++) {
int yint = round(y);
// afișează pixelul (x, yint)
y += panta;
}
Pentru următoarea variantă, nu mai reținem coordonata reală y, ci coordonata întreagă și abaterea dintre cele două, care va fi mereu cuprinsă între -0.5 și 0.5. Nu obținem nicio îmbunătățire de viteză, dar pregătim terenul pentru ultima variantă, care operează doar pe variabile întregi.
double p = (double)(y2 - y1) / (x2 - x1);
double abatere = 0.0;
int y = y1;
for (int x = x1; x <= x2; x++) {
// afișează pixelul (x, y)
abatere += panta;
if (abatere > 0.5) {
y++;
abatere -= 1;
}
}
În sfârșit, dorim să înlocuim variabilele reale p și abatere cu variabile întregi. Pentru acestea, amplificăm toate operațiile pe ele cu x2 - x1. Atunci p devine y2 - y1. Atenție, și constantele 0.5 și 1 trebuie amplificate! Iar pentru a elimina constanta 0.5, amplificăm testul de inegalitate cu 2.
int abatere = 0;
int y = y1;
for (int x = x1; x <= x2; x++) {
// afișează pixelul (x, y)
abatere += y2 - y1;
if (2 * abatere > x2 - x1) {
y++;
abatere -= x2 - x1;
}
}
Observăm că acum abaterea va fi mereu cuprinsă între . Pentru maximum de eficiență, înmulțirea cu 2 poate fi exprimată ca shiftare, iar cantitățile x2 - x1 și y2 - y1 pot fi precalculate în afara buclei.
Înfășurătoarea convexă
Definiție: înfășurătoarea convexă a unei mulțimi de n puncte este cel mai mic poligon convex care include toate punctele. Vizual, dorim să construim un „gard” în jurul mulțimii. Acest gard se sprijină pe unele dintre puncte. Soluția cere, în general, enumerarea acestor puncte în ordine (trigonometrică sau orară).
Pentru simplitate, considerăm că oricare trei puncte sunt necoliniare.
Algoritmul naiv
Observăm că înfășurătoarea convexă constă din segmente cu capetele în punctele mulțimii. Pentru un astfel de segment, toate celelalte n - 2 puncte sunt de aceeași parte a dreptei. Așadar:
- Pornim cu punctul A având coordonata y minimă. Acest punct este sigur pe înfășurătoare.
- Căutăm un punct B astfel încât toate punctele în afară de A și B să se afle de aceeași parte a dreptei AB.
- Facem aceasta înlocuind fiecare punct P în ecuația dreptei AB și observând ce semn obținem.
- Căutăm un punct C astfel încât toate punctele în afară de B și C să se afle de aceeași parte a dreptei BC.
- Când ajungem înapoi în punctul A, am găsit înfășurătoarea ABC...A.
Algoritmul are complexitatea O(h n2), unde h este numărul de puncte de pe înfășurătoarea rezultată. Dacă h este O(n), algoritmul este O(n3).
De expandat: algoritmul gift wrapping, numit și marșul lui Jarvis.
Algoritmul Graham scan
Putem îmbunătăți algoritmul naiv folosind o stivă ordonată. Stiva va conține o succesiune de puncte care descriu în permanență o curbă convexă.
Algoritmul pornește de la punctul A de coordonată y minimă și sortează restul punctelor, Pi după unghiul format de PiA cu axa Ox. În mod garantat, A și P0 fac parte din înfășurătoarea convexă.
Cum impunem convexitatea punctelor din stivă? Dorim ca traiectoria formată, în ordine, de ultimele trei puncte din stivă să cotească spre stânga. Dacă inserăm un punct care cauzează o curbă spre dreapta, punctul anterior lui trebuie eliminat din stivă. În mod sigur, A, P0 și P1 vor coti spre stânga.
Așadar:
schimbă p[0] cu punctul de y minim;
sortează punctele p[1]...p[n-1] după unghiul format de p[i]p[0] cu orizontala;
s = stivă goală
push(s, p[0]);
push(s, p[1]);
push(s, p[2]);
for (i = 3; i < n; i++) {
while (laDreapta(penultim(s), top(s), p[i])) {
pop(s);
}
push(s, p[i]);
}Rutina laDreapta() folosește testul de orientare predat anterior.
Complexitatea algoritmului este O(n log n) din cauza sortării. Dacă punctele sunt deja sortate, algoritmul merge în O(n). Remarcați că stiva ordonată este un principiu care revine obsesiv de frecvent, aproape la fiecare lecție.
Lăsăm ca temă de cercetare individuală sortarea polară (unghiulară) a punctelor. Indiciu: deoarece am ales p[0] cu y minim, unghiurile vor fi cuprinse între 0 și 180 de grade. Funcția cosinus este monoton descrescătoare pe acest interval.






























