Clasa a VI-a lecția 37 - 29 mai 2019
Tema - rezolvări
Rezolvări aici: [1]
Lecție
<html5media height="720" width="1280">https://www.algopedia.ro/video/2018-2019/2019-05-29-clasa-6-lectie-info-37-720p.mp4</html5media>
Funcții în limbajul C
Funcțiile permit programelor complicate să fie parcelate în blocuri mici, fiecare din ele fiind mai ușor de scris, citit și modificat (întreținut). Am întîlnit deja funcția main() și am folosit funcții de intrare ieșire precum fscanf() și fprintf(), precum și funcții matematice din bibliotecile standard precum sqrt() sau abs(). Vom vedea în continuare cum putem să scriem propriile noastre funcții.
De ce funcții
- Pentru a nu repeta cod.
- Pentru organizare, citibilitate, ușurinta înțelegerii codului și întreținerea codului.
- Recursivitate, precum vom vedea anul următor.
Sintaxa: cum scriem o funcție
Sintaxa (simplificare)
tip-returnat nume-funcție( tip-1 param-1, tip-2 param-2, ..., tip-n param-n ) { ... declarații variabile ... ... cod funcție ... return valoare-return; // dacă tipul returnat nu este 'void' }
Exemplu
// functie ce returnează valoarea minima dintre două numere
int min(int a, int b) {
int rezultat; // declaratie de variabila locala
if (a < b)
rezultat = a;
else
rezultat = b;
return rezultat;
}Apelul
O funcție este apelată astfel:
Apelul funcțiilor
Pentru a apela (sau chema) o funcție vom scrie numele funcției urmat, între paranteze, de parametrii ceruți. Ei pot fi expresii, nu doar variabile. Expresiile se vor apela, iar rezultatele lor vor fi depuse, la intrarea în funcție, în variabilele parametru corespunzătoare, conform ordinii din listă. Dacă funcția returnează o valoare ea poate fi folosită sau stocată într-o variabilă:
rez = nume-functie( valoare-1, valoare-2, ..., valoare-n );
Iată un exemplu de folosire a funcției min():
#include <stdio.h>
// functie ce returnează valoarea minima dintre două numere
int min(int a, int b) {
int rezultat; // declaratie de variabila locala
if (a < b)
rezultat = a;
else
rezultat = b;
return rezultat;
int main () {
int x, y, rez;
x = 200;
y = 100;
rez = min( x, y ); // chemam functia pentru a obtine valoarea minima
printf( "Valoarea minima este: %d\n", rez );
return 0;
}Parametri și valoare returnată
Precum am văzut, o funcție primește o listă de parametri și returnează o valoare. Funcția poate să nu returneze nici o valoare, caz în care tipul returnat va fi declarat ca void, sau "vid" în limba engleză.
Atenție: transmisia parametrilor în funcție se face prin copiere! Aceasta înseamnă că la apelul funcției valorile din apel vor fi atribuite parametrilor ce sînt variabile nou create ce primesc acele valori.
Exemplul 1: ce afișează următorul program:
void inc( int a ) {
a++;
}
int main() {
int x;
x = 0;
inc( x );
printf( "%d\n", x );
return 0;
}Parametrul a este o variabilă nou creată la intrarea în funcție în care se copiază valoarea variabilei x. Funcția modifică (incrementează) valoarea lui a, dar aceasta nu influențează valoarea lui x, ele fiind variabile diferite. De aceea programul va afișa 0.
Exemplul 2: ce afișează următorul program:
void inc( int a[10] ) {
a[0]++;
}
int main() {
int v[10];
v[0] = 17;
inc( v );
printf( "%d\n", v[0] );
return 0;
}Surpriză, programul va afișa 18! Elementul zero al vectorului a fost modificat. Și atunci cum rămîne cu transmisia prin copiere? Răspunsul este greu de dat fără cunoștințe despre pointeri. Vectorii sînt ei înșiși adrese de variabile întregi. Parametrul vector se transmite prin copiere, însă ceea ce se copiază este adresa unde se află șirul de întregi ai vectorilor. De aceea modificarea unui vector într-o funcție are ca efect modificarea vectorului.
Pentru moment este deajuns să țineți minte că variabilele simple se transmit prin copiere, iar vectorii (matricele, etc) se transmit ca atare, fără a fi copiați.
Cum transmitem corect vectorii unei funcții
Un vector este un tip de date abstract care constă dintr-o pereche (n, v). n este lungimea vectorului (numărul de elememente), iar v este vectorul propriu zis. Ele nu se pot separa. De aceea vom transmite funcției atît vectorul cît și lungimea sa.
Exemplu: suma elementelor unui vector
#include <stdio.h>
int sumaVect( int n, int v[] ) {
int i, s;
s = 0;
for ( i = 0; i < n; i++ )
s += v[i];
return s;
}
int main() {
int x;
int a[10] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
x = sumaVect( 10, a );
printf( "Suma este %d\n", x );
return 0;
}Modificarea numărului de elemente al vectorului într-o funcție
Ce se întîmplă dacă funcția modifică numărul de elemente al vectorului, de exemplu inserează un element în vector? Ar trebui să modificăm numărul de elemente, ceea ce nu putem face în funcție, din cauza transmiterii prin copiere a parametrilor. O soluție poate fi ca funcția să returneze noul număr de elemente al vectorului.
Exemplu: ștergerea unei valori din vector
#include <stdio.h>
// sterge valoarea e din v[] de pe toate pozitiile unde apare
int stergVect( int n, int v[], int e ) {
int i, j;
j = 0;
for ( i = 0; i < n; i++ )
if ( v[i] != e ) {
v[j] = v[i];
j++;
}
return j;
}
int main() {
int n, i;
int a[10] = { 1, 2, 3, 4, 2, 3, 2, 8, 9, 2 };
n = 10;
n = stergVect( n, a, 2 );
printf( "Vectorul are acum %d elemente:", n );
for ( i = 0; i < n; i++ )
printf( " %d", a[i] );
printf( "\n" );
return 0;
}Programul va afișa:
Vectorul are acum 6 elemente: 1 3 4 3 8 9
Pentru matrice cărora funcția le modifică dimensiunile vom vedea mai jos cum putem proceda.
Exemple
Scrieți funcții care să rezolve:
Inversare vector
#include <stdio.h>
// inverseaza (rastoarna) elementele unui vector
void invVect( int n, int v[] ) {
int i, j, aux;
i = 0;
j = n - 1;
while ( i < j ) {
aux = v[i];
v[i] = v[j];
v[j] = aux;
i++;
j--;
}
}
int main() {
int n, i;
int a[10] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
n = 10;
invVect( n, a );
printf( "Vectorul inversat este:" );
for ( i = 0; i < n; i++ )
printf( " %d", a[i] );
printf( "\n" );
return 0;
}Inserare element în vector la o poziție dată
#include <stdio.h>
// insereaza un element e in vectorul v de n elemente la pozitia poz
// daca poz este mai mare strict decit n nu face nimic
int insVect( int e, int n, int v[], int poz ) {
int i;
if ( poz <= n ) { // putem insera?
for ( i = n; i > poz; i-- )
v[i] = v[i - 1];
v[poz] = e;
n++;
}
return n;
}
int main() {
int n, e, i;
int a[20] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
n = 10;
e = 15;
n = insVect( e, n, a, 5 ); // insereaza 15 pe pozitia 5
printf( "Vectorul cu %d inserat pe pozitia 5 este:", e );
for ( i = 0; i < n; i++ )
printf( " %d", a[i] );
printf( "\n" );
return 0;
}Citire întreg fără semn din fișier folosind doar fgetc()
#include <stdio.h>
#include <ctype.h> // pentru isdigit()
FILE *fin;
// Citeste un intreg de la intrare
int getInt() {
int ch, n;
n = 0;
while ( !isdigit( ch = fgetc( fin ) ) ); // ignora non-cifre
do n = n * 10 + ch - '0';
while ( isdigit( ch = fgetc( fin ) ) );
return n;
}
// Citim un vector din fisierul 'fin' si il afisam
int main() {
int n, i;
int v[20];
fin = fopen( "exemplu.in", "r" );
n = getInt();
for ( i = 0; i < n; i++ )
v[i] = getInt();
fclose( fin );
printf( "Vectorul citit este:" );
for ( i = 0; i < n; i++ )
printf( " %d", v[i] );
printf( "\n" );
return 0;
}Observați că am declarat variabila fișier în afara lui main() pentru a putea fi vizibilă în funcție. Vom vorbi despre aceasta mai jos.
Reguli de vizibilitate ale variabilelor în funcții
În C avem două tipuri de variabile: locale și globale.
- Variabilele locale se declară în interiorul unei funcții (sau în interiorul lui
main()) și sînt vizibile (apelabile, folosibile) doar în acea funcție. Se cheamă că variabilele aparțin acelei funcții. - Variabilele globale se declara în afara oricărei funcții și sînt vizibile din toate funcțiile, inclusiv
main(). Precum știm deja ele sînt și inițializate automat cu zero.
Ce se întîmplă dacă denumim o variabilă locală cu același nume ca una globală? Cea locală are prioritate.
Exemplu
Ce afișează următorul program?
#include <stdio.h>
int a = 100; // declarare variabila globala
void afiseaza() {
printf( "a global este %d\n", a );
}
int main () {
int a; // declarare variabila locala cu acelasi nume
a = 30; // atribuire variabila locala
afiseaza();
printf( "a local este %d\n", a );
return 0;
}Programul va afișa:
a global este 100 a local este 30
Modificarea parametrilor cu efect la ieșirea din funcție
Ce facem dacă totuși ne dorim să modificăm o variabilă transmisă ca parametru? În acest caz vom apela funcția cu adresa de memorie (zisă și pointer) a variabilei. Vom folosi doi operatori noi:
- & se aplică unei variabile și extrage adresa de memorie a variabilei
- * se aplică unei adrese de memorie și extrage conținutul variabilei de la acea adresă
Ar fi bine să evitați, deocamdată, deoarece mai întîi trebuie să învățați noțiunea de pointeri, care nu face scopul acestei lecții.
Exemplu: functia swap
#include <stdio.h>
void swap( int *pa, int *pb ) {
int aux;
aux = *pa;
*pa = *pb;
*pb = aux;
}
int main() {
int a, b;
a = 100;
b = 200;
swap( &a, &b );
printf( "a=%d b=%d\n", a, b );
return 0;
}- Declarații de variabile și vizibilitatea acestora. Așezarea lor pe stivă.
- Conversia de tip cînd chemăm funcția cu alte tipuri decît cele declarate.
Funcțiile și programarea structurată
Instrucțiunea return este echivalentul unui salt la finalul funcției. Programare evident nestructurată. De aceea, deși limbajul C ne permite, nu o vom folosi decît la finalul funcției, ca ultima instrucțiune. C este un limbaj vechi. Limbaje gen Pascal au rezolvat problema nestructurării eliminînd instrucțiunea return.
Cînd scriem funcții?
Bun, am învățat funcții. Dar cum iau decizia să scriu o funcție sau nu?
- Atunci cînd nu putem evita repetiția de cod prin alte mijloace (factorizare, bucle, etc)
- Atunci cînd programul devine prea lung pentru a fi citit ușor, de obicei undeva la 80-100 de linii. Ca regulă generală o funcție ar fi bine să aibă pînă în 100 de linii, dar desigur regula nu este bătută în cuie.
- Atunci cînd simțim că o bucată semnificativă de cod are o coeziune, reprezintă un tot unitar, o putem transforma în funcție.
- Atunci cînd scriem o bucată de cod care execută un calcul general, gen sortare, sau citirea unui întreg, atunci o putem scrie ca funcție pentru a o refolosi în viitor. Vom vedea că aceasta este baza de pornire a bibliotecilor de funcții.
- Nu este bine să "rupem" artificial programul de dragul funcțiilor. Dacă tot programul ar avea 40 de linii, introducerea unor funcții i-ar scădea lizibilitatea.
- Pe cazul general, la olimpiade și pentru programele mici care rezolvă probleme de concurs încercați să evitați funcțiile inutile, doar de dragul artei. Cînd tot programul, scris elegant, ar avea 80 de linii este destul de greu să justifici introducerea unor funcții.
Cum denumim funcțiile?
O funcție trebuie denumită cît mai sugestiv. Funcții denumite citire() sau solve() cu am văzut la colegii voștri mai mari fac codul mai necitibil decît dacă ele nu existau. Ele sînt echivalentul variabilelor denumite contor sau stegulet. Așa cum stegulețul ar fi bine să se numească terminat sau fara_zero, la fel și funcțiile trebuie denumite sugestiv. Pentru cele două funcții de mai sus nume bune ar fi citesteVectorInaltimi() sau calculSumePartiale(). Observați că primul cuvînt din denumirea unei funcții începe cu literă mică, celelalte cu literă mare. Aceasta este o convenție de codare. Pentru variabile formate din mai multe cuvinte vom folosi numai litere mici, unind cuvintele cu underscore (sau underline, caracterul '_').
Considerente de viteză
Atunci cînd funcția poate fi chemată de un număr mare de ori calculatorul pierde un timp semnificativ în apelul de funcție. Un exemplu tipic ar fi cînd funcția este chemată într-o buclă care se execută de un milion de ori. Ce putem face?
- Evitați astfel de funcții, dacă nu dăunează eleganței și citibilității programului: introduceți codul funcției în loc de apel.
- Dacă totuși trebuie să folosiți o funcție aveți opțiunea să o declarați inline. Aceasta înseamnă că compilatorul nu va genera cod care să cheme funcția ci va înlocui apelul cu chiar corpul funcției, peste tot unde apare el. Este ca și cum funcția nu ar exista, păstrînd însă citibilitatea programului (nu și scurtimea executabilului generat, din păcate).
Despre măsurarea timpului
Cum măsurăm timpul. Articolul principal este aici: Testarea timpului de execuție al unui program
Programarea logicii jocurilor de strategie cu informație completă
Vom discuta cum putem programa logica mutărilor pentru jocuri de doi jucători de genul X și 0, șah, reversi, dame, etc. Ceea ce vom învăța se aplică și la Pah-Tum.
Arbori de joc
Atunci cînd jucăm un astfel de joc analizăm mutările posibile. Pentru fiecare din mutări analizăm ce mutări posibile are adversarul. Iar pentru fiecare din mutările adversarului vedem ce mutări posibile avem noi. Și tot așa. Să luăm de exemplu jocul X și 0. Analiza noastră poate fi reprezentată ca un arbore desenat invers, cu rădăcina în sus.
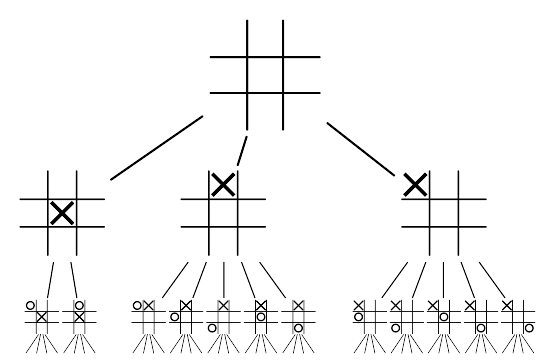
La fiecare poziție pe tablă am desenat toate mutările posibile și noile poziții la care se ajunge în urma lor. Acest arbore arată două semi-mutări, sau, în engleză, plies (one ply two plies).
Dacă am continua astfel am obține un arbore complet ce conține toate cele 765 poziții unice ce pot apărea în timpul jocului (ignorînd rotațiile și transpunerile). Ar fi un arbore foarte mare, dar odată completat am putea să mergem pe niveluri, de jos în sus, și să aflăm care este mutarea perfectă în oricare din pozițiile intermediare. În acest caz frunzele (terminațiile) arborelui sînt poziții de final, în care unul din jucători cîștigă, sau este remiză. În mod cert, în orice poziție jucătorul care este la mutare va alege mutarea cea mai bună pentru el. Să etichetăm frunzele cu 1 dacă X cîștigă, -1 dacă 0 cîștigă, respectiv 0 dacă este remiză. Atunci, pentru orice poziție din arbore, dacă X este la mutare el va alege din mutările posibile pe cea maximă, în vreme ce 0 o va alege pe cea minimă. Cu acest număr, maxim sau minim, vom eticheta poziția curentă din arbore. Etichetarea pornește de jos în sus.
Pentru X și 0 știm că, dacă ambii jucători joacă perfect, jocul se termină prin remiză, așa încît dacă vom eticheta pozițiile din arbore de jos în sus este clar că poziția rădăcină, tabla goală, va avea etichetă 0, echivalentă remizei.
Observație: primele etichete calculate sînt cele ale frunzelor, pe baza jucătorului care cîștigă. Celelalte poziții primesc etichete calculate pe baza maximului sau minimului dintre pozițiile de sub ele. Spunem că "propagăm" aceste numere în susul arborelui.
Pentru alte jocuri arborele complet al jocului este foarte mare. Nu avem timpul necesar pentru a analiza toate nodurile, iar dacă am încerca să îl stocăm nu am avea destulă memorie. Ce putem face în acest caz?
Algoritmul minimax
La jocul de șah avem, pe medie, circa 38 de mutări posibile în deschidere. Aceasta înseamnă că după un ply vom avea circa 38 de poziții posibile, după două plies vom avea 382, după trei plies 383 poziții și așa mai departe. Numărul de poziții din arbore crește foarte repede.
Arborele parțial de joc
Ideea veteranului algoritm minimax este să analizăm un arbore parțial. Să spunem că fixăm o adîncime maximă d=3. Aceasta înseamnă că vom eticheta arborele ce analizează trei plies (semi-mutări) în avans. Apoi procedăm similar cu cazul cînd avem arborele complet: etichetăm frunzele, adică pozițiile aflate la trei semi-mutări adîncime cu anumite scoruri. Apoi propagăm acele scoruri în sus după aceeași regulă, calculînd minimul sau maximul în funcție de cine este la mutare. Iată un exemplu, pentru jocul de X și 0, în care nu am mai desenat pozițiile la nivel 3 (frunze) din lipsă de spațiu:
Observăm că scorul maxim posibil este 7 și este dat de prima mutare (în centru). Ce reprezintă acest scor?
Scorul minimax este scorul garantat pe care îl poate obține jucătorul la mutare după d plies indiferent de mutările adversarului. Aceasta înseamnă că, în funcție de ceea ce joacă adversarul, este posibil ca la adîncime d jucătorul la mutare să obțină un scor mai mare.
Cum etichetăm frunzele, pozițiile cele mai de jos în arbore, aflate la semi-mutare d?
Evaluarea statică
Scorul pe care îl vom atribui pozițiilor frunză va fi o estimare asupra a cît de bine stă jucătorul aflat la mutare inițial (X în cazul lui X și 0). Această estimare se numește evaluare statică deoarece ea ține cont doar de proprietățile poziției curente. Nu vom încerca să simulăm mutări, deoarece de acest lucru se ocupă algoritmul minimax.
Cum evaluăm static o poziție? Vom ține cont de mai multe proprietăți semnificative ale unei poziții. Să luăm niște exemple:
- La șah vom ține cont de:
- Avantajul material: valoarea însumată a tuturor pieselor mele, măsurată în echivalentul unui pion, minus valoarea însumată a pieselor adversarului.
- Diverse avantaje poziționale: pioni legați, sau trecuți, rege bine ferit, piese mobile (care au multe posibilități de a muta), etc.
- La X și 0 am putea ține cont de:
- Centralitatea pieselor.
- Numărul de linii/coloane/diagonale pe care X are piese minus numărul de linii/coloane/diagonale pe care 0 are piese.
- Numărul de linii, coloane sau diagonale unde X mai poate forma trei în linie, minus numărul de linii, coloane sau diagonale unde 0 mai poate forma trei în linie.
Astfel, putem da scoruri pentru fiecare din criterii. Scorul final va fi o sumă a acestor scoruri parțiale înmulțite cu ponderi. De exemplu, la X și 0 am putea să adunăm numărul de linii unde mai poate forma trei în linie înmulțit cu 10, cu numărul de linii ocupate înmulțit cu 3.
Implementarea algoritmului
O implementare accesibilă la nivelul clasei a șasea poate proceda astfel: - Fixăm un nivel de adîncime, cel mai probabil d=4 sau d=5. - Pentru o poziție vom folosi o buclă în care vom genera toate mutările valide. În realitate bucla aceasta va fi probabil formată din două bucle care parcurg tabla ca o matrice, pe linii. - Pentru adîncimea noastră, să zicem 4, vom avea patru bucle imbricate (una într-alta) în care vom genera toate mutările posibile pînă la adîncime patru. Vom avea grijă să plasăm piesele pe tablă atunci cînd analizăm mutarea și să le ridicăm de pe tablă cînd revenim și încercăm altă mutare. - În bucla interioară (ce nu mai are altă buclă în ea) pentru fiecare mutare vom evalua static poziția la care s-a ajuns. - În celelalte bucle, la fiecare mutare (și poziție rezultată în urma ei) vom primi un scor, pe care îl vom compara cu scorul maxim obținut pînă acum (sau minim dacă adversarul execută mutarea). Scorul maxim obținut va fi raportat la bucla imediat de mai sus.
De exemplu, pentru adîncime trei algoritmul va arăta astfel:
- Citește tabla de la intrare și determină cine este la mutare
- scor1 = -∞
- Pentru fiecare mutare posibilă a mea la adîncime 1
- Execută acea mutare (pune piesa pe tablă)
- scor2 = +∞
- Pentru fiecare mutare posibilă a adversarului la adîncime 2
- Execută acea mutare
- scor3 = -∞
- Pentru fiecare mutare posibilă a mea la adîncime 3
- Execută acea mutare
- s = evalStatic(poziția curentă)
- Dacă s > scor3 atunci scor3 = s
- Retrage mutarea făcută la adîncime 3 de pe tablă
- Dacă scor3 < scor2 atunci scor2 = scor3
- Retrage mutarea făcută la adîncime 2 de pe tablă
- Dacă scor2 > scor1 atunci scor1 = scor2 și păstrează mutarea care a dus la acest scor în M
- Retrage mutarea făcută la adîncime 1 de pe tablă
- Mută mutarea găsită, M
- Afișează noua tablă
Pentru adîncimi mai mari veți adăuga corespunzător bucle. Dacă veți scrie funcția de evaluare eficient ar trebui să puteți merge pînă la adîncime cinci. Dacă nu, mergeți pînă la adîncime patru.
Idei de evaluare statică a poziției la Pah-Tum
Precum spuneam, scorul static al unei poziții pe tablă va ține cont de multe scoruri mai mici acordate după diverse criterii. Aici puteți avea foarte multe idei originale și este locul unde vă puteți evidenția față de ceilalți concurenți. Să enumerăm cîteva idei:
- Material: scorul curent al meu minus scorul curent al adversarului pe tablă.
- Pentru fiecare linie sau coloană putem acorda scoruri pentru cît aș obține dacă aș umple golurile cu piesa mea minus cît ar obține adversarul dacă ar umple golurile cu piesa sa.
- Pentru fiecare piesă (a mea sau a adversarului) pot acorda un scor pentru centralitate. O piesă centrală este, probabil, mai bună.
- Putem să simulăm un mini-joc de Pah-Tum pe fiecare linie sau coloană! Arborele fiind mic (cîte frunze are el?) îl putem calcula complet. În fapt putem calcula toate pozițiile posibile la început și le putem da scoruri pe care le vom stoca într-un vector. Apoi dăm acel scor liniilor pe care le întîlnim pe tabla curentă.
- Alte idei: descriere programe participante la un turneu de Pah-Tum.
Indiferent ce scoruri parțiale veți alege, ele se vor înmulți cu numere ponderi și apoi se vor aduna în scorul final. Arta voastră va fi să reglați aceste ponderi pentru un joc cît mai bun (după ce alegeți criteriile de scor).
Mai multe detalii găsiţi la lecţia de clasele 9/10: Note de curs, clasele 9-10, 22 mai 2014.
Temă
Rezolvați problemele date la ONI 2019. Încercați să nu repetați cod, folosind funcții acolo unde are sens. Nu forțați, dacă nu vi se pare că are sens să folosiți funcții, mai bine nu folosiți.
Atenție: tema nu are penalizări pentru mai multe submisii.
- maya dată la ONI 2019 clasa a 6a
- optime dată la ONI 2019 clasa a 6a
- roata1 dată la ONI 2019 clasa a 6a
Rezolvări aici [2]
- Continuați programarea la jocul Pah-Tum folosind ceea ce ați învățat azi. Nu uitați să vă înscrieți cît mai repede la concurs, nu e nevoie să aveți programul!
- Opțional: puzzle: avem 12 bile care arată identic, una este ușor diferită (mai ușoară sau mai grea, nu se știe). Avem la dispoziție o balanță. Găsiți bila diferită din trei cîntăriri, aflînd și dacă este mai grea sau mai ușoară.
- Opțional: puzzle: ziua regelui: un rege organizează o petrecere mare de ziua lui. Petrecerea începe peste 24 de ore. Regele află că una din cele 1000 de sticle de vin pe care le va servi este otrăvită. Otrava acționează ciudat: omul care bea chiar și cea mai mică cantitate din această otravă nu are nici un simptom vreme de 24 de ore, apoi moare subit. Regele are sclavi la dispoziție pe care îi poate folosi. Lui nu îi pasă cîți sclavi mor, dar îi pasă cîți sclavi beau vin, deoarece un sclav care a băut vin nu poate fi folosit la treabă, ci trebuie izolat spre observare. Care este numărul minim de sclavi cu care regele poate afla sticla otrăvită în cele 24 de ore pe care le are la dispoziție?
